円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係
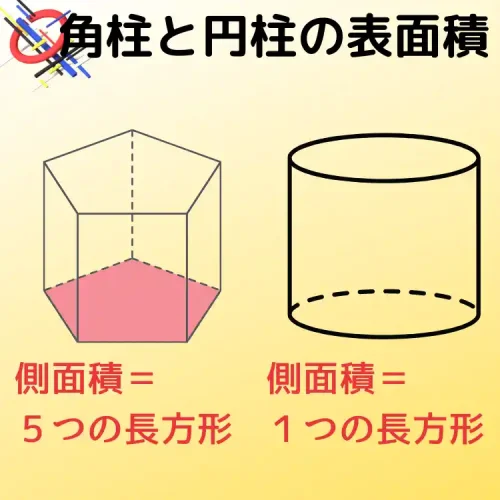
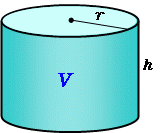
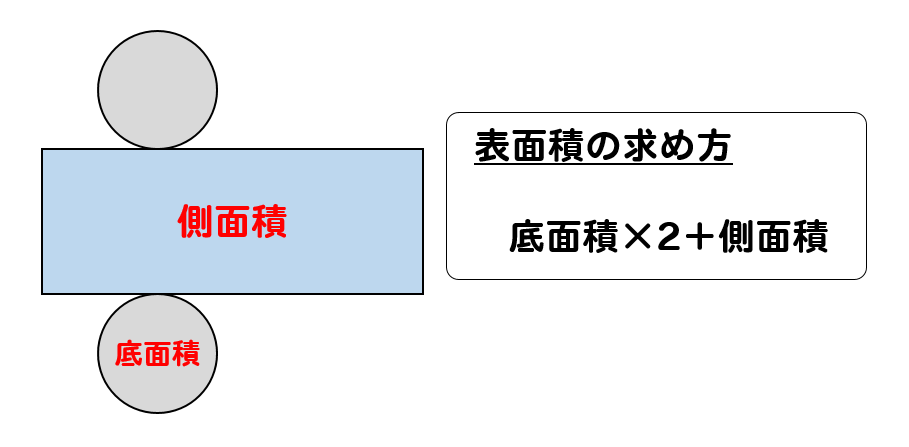
角柱や円柱の表面積を出すには、上下2つの底面積と側面積を計算した後、数字を足すのです。 そのため、柱体の表面積の公式は以下のようになります。 柱体の表面積 = 底面積 × 2 + 側面積それでは、円柱の体積の求める公式を説明していきましょう。 円柱の体積 (V)=πr²h→円柱の体積 (V)=底面の円の面積 (πr²)×高さ (h)→底面の円の面積=半径 (r)×半径 (r)×円周率 (π) となります
円柱 の面積 公式
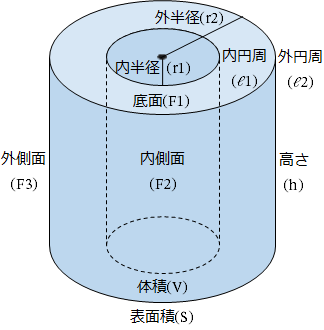
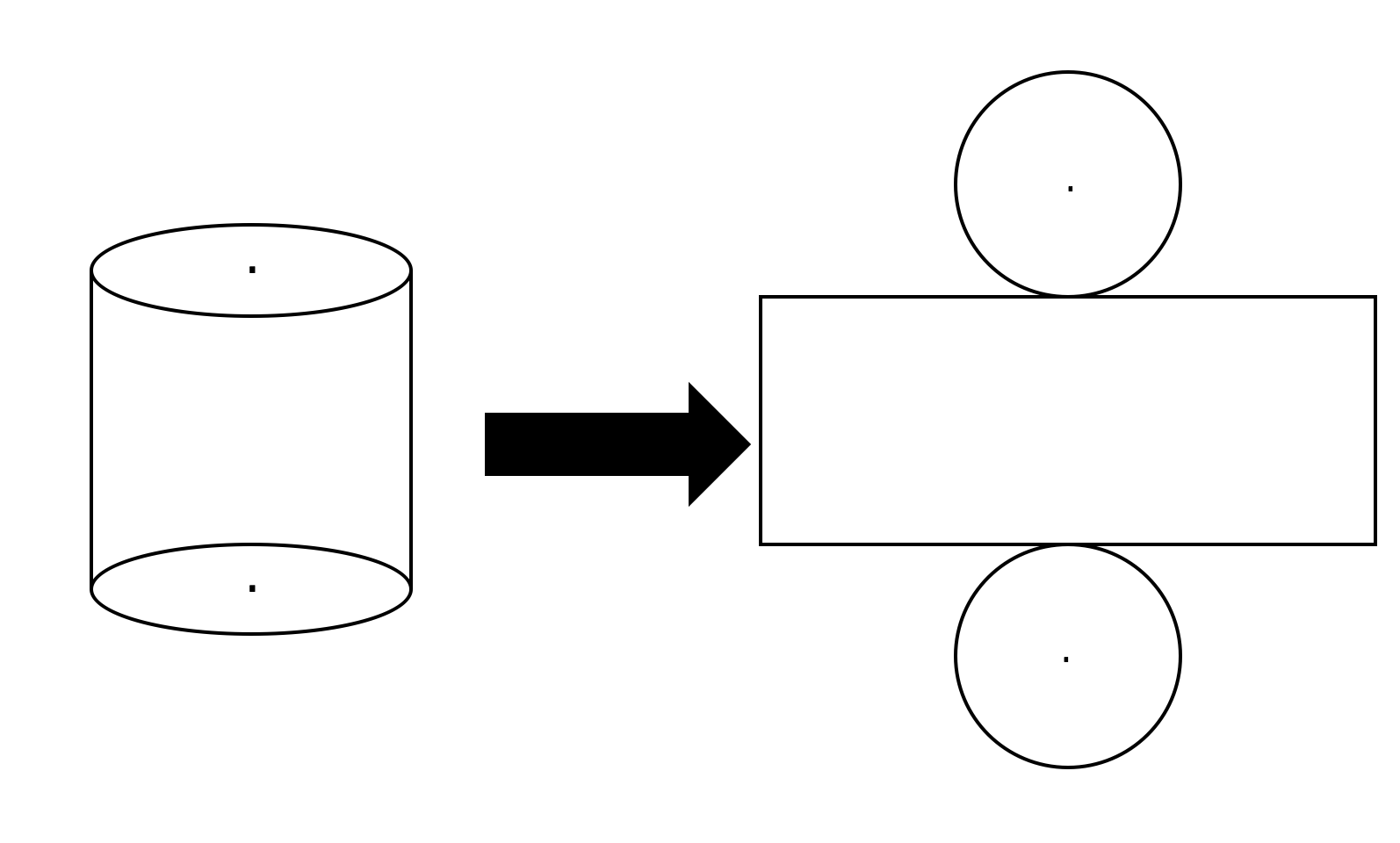
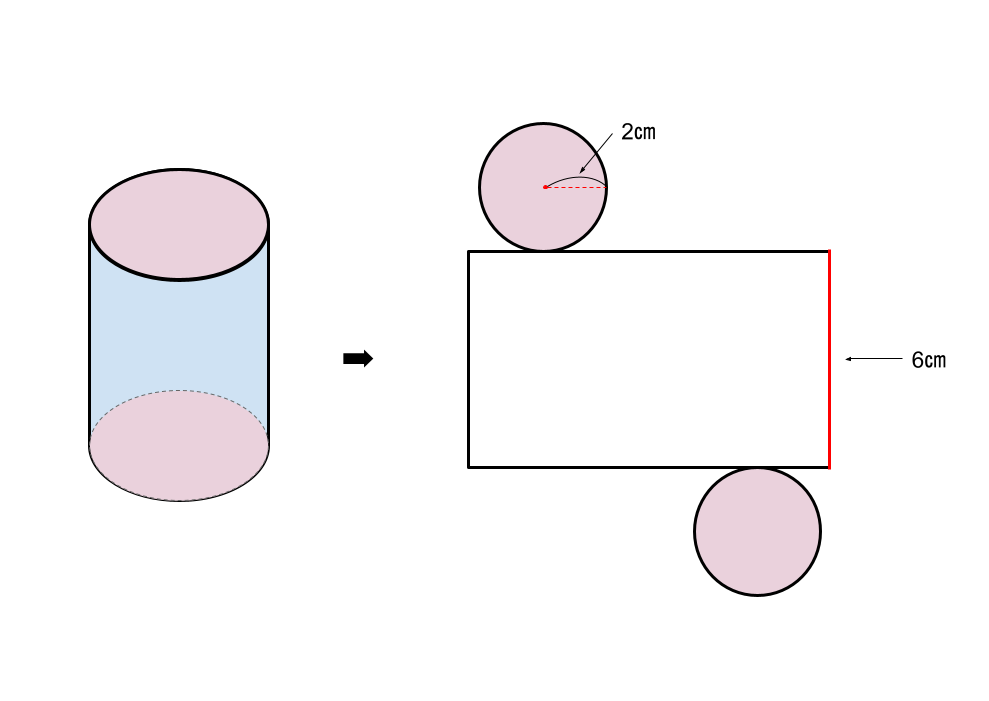
円柱 の面積 公式-中空円の面積の求め方はS=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか? keisanより 円の直径 = 2 * 円の半径 より、 円つまり、円柱の表面積を求めるには、2つの合同な円(2つの底面)と、長方形(側面)の面積を足せばよいのです。 円柱の表面積をS₁、底面の面積をS₂、側面の面積をS₃、半径を r 、円周率を π 、
Q Tbn And9gctm68kdraeqpo Giyvxsau9prclg93urr7 Jafgpxhgzzohnnqrfkmb Usqp Cau
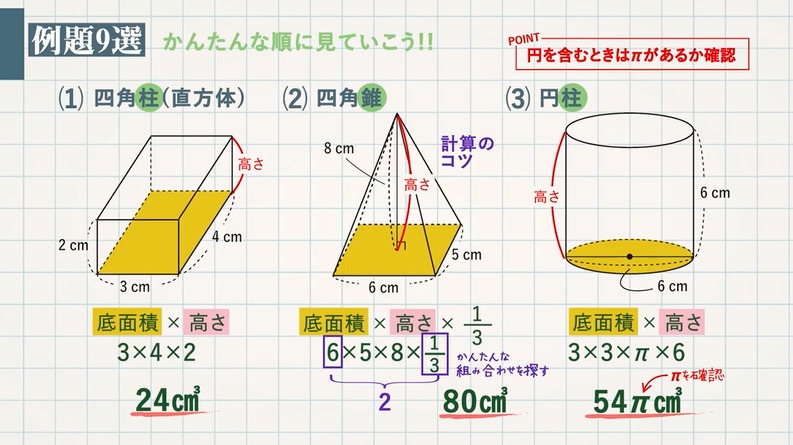
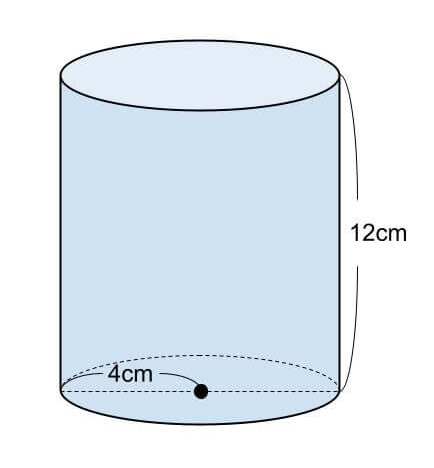
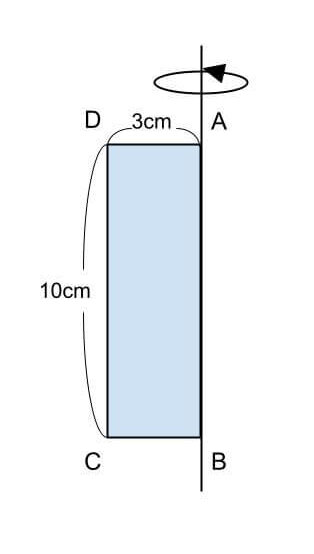
円柱の表面積が㎠、底面の円の半径が4cmの円柱の高さを求めましょう。 (円周率は314とします。 ) この円柱の展開図は次のようになります。 円柱の表面積-2つの円の 円柱の公式(計算式) 円柱の体積V V = πr2h V = π r 2 h 円柱の表面積S S = 2πr(r h) S = 2 π r r h 円柱の側面積F F = 2πrh F = 2 π r h ホーム かんたん計算機側面の面積=6cm×8πcm=48πcm 2 円柱の面積=16πcm 2 16πcm 2 48πcm 2 =80πcm 2 数式で計算する場合は、半径をr・高さをh・円周率をπとすると、 (r 2×π×2) (2×r×π×h) となり、まとめ
円柱 の面積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円柱 の面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |





0 件のコメント:
コメントを投稿